806. Platforms - 3

In older games one can run into the next situation. The hero jumps along the platforms that hang in the air. He must move himself from one side of the screen to the other. When the hero jumps from one platform to the neighboring, he spends |y₂ – y₁|² energy, where y₁ and y₂ are the heights where these platforms hang. The hero can make a super jump that allows him to skip one platform, but it takes him 3 * |y₃ – y₁|² energy.

You are given the heights of the platforms in order from the left side to the right. Find the minimum amount of energy to get from the 1-st (start) platform to the n-th (last).

Input. The first line contains the number of platforms n (2 ≤ n ≤ 10⁵). The second line gives n integers – the heights of the platforms. Their absolute values are not grater than 4000 by absolute value.

Output. Print one integer – the minimum amount of energy.

Sample input	Sample output
4 1 2 3 30	731

SOLUTION

dynamic programming

Algorithm analysis

With given energy functions sometimes it is optimal for the hero to make one move backwards. Consider the following example. Suppose we have 4 platforms with heights of 1, 10, 2, 11. We calculate the energy that hero should spent to reach the last platform in different ways.

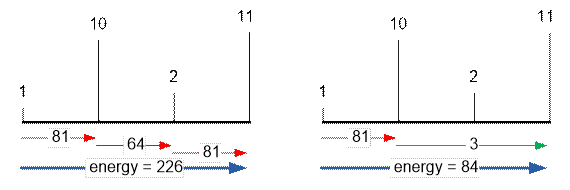
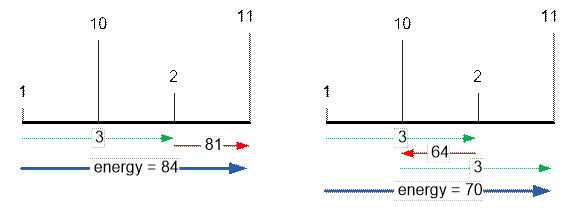
As we can see, the optimal way is to jump from 1-st platform to the 3-rd using super jump, then return to the 2-nd and using super jump once more, to appear on the last, 4-th platform. The total spent energy equals to 3 + 64 + 3 = 70.

Let dp[i] be the minimal amount of energy enough to get from the 1-st platform to the i-th. Let dp[1] = 0, because initially we are on the first platform. We can get to the second platform either from the first only (if n = 2), or in two ways:

· from 1-st to the 2-nd using |y₂ – y₁|² energy;

· from 1-st to the 3-rd and then to the 2-nd spending 3 * |y₃ – y₁|² + |y₂ – y₃|² energy;

So if n > 2 then dp[2] = min(|y₂ – y₁|², 3 * |y₃ – y₁|² + |y₂ – y₃|²).

Now consider the calculation of dp[i]. One can get into i-th platform either from (i – 1)-th or from (i – 2)-th using super jump. But when i < n, one can get into the i-th platform from the (i + 1)-th, where we jumped from the (i – 1)-th. So dp[i] equals to minimum among the values:

· dp[i – 1] + |y_i – y_i-1|² : normal jump from the (i – 1)-th platform;

· dp[i – 2] + 3 * |y_i – y_i-2|² : super jump from the (i – 2)-th platform;

· dp[i – 1] + 3 * |y_i+1 – y_i-1|² + |y_i – y_i+1|² : one jumps from the (i – 1)-th to (i + 1)-th, and then to i-th platform. This movement possible only if i < n.

Algorithm realization

The heights of platforms are stored in array а. In array dp we keep the optimal energies.

#define MAX 100010

long long a[MAX], dp[MAX];

Declare the function sq that computes the square of a number.

long long sq(long long a)

{

return a * a;

}

Read the input data.

scanf("%d", &n);

for(i = 1; i <= n; i++)

scanf("%lld", &a[i]);

Initialize the values dp[1] and dp[2].

dp[1] = 0;

if (n == 2) dp[2] = sq(a[2] - a[1]);

else dp[2] = min(sq(a[1] - a[2]), 3 * sq(a[1] - a[3]) + sq(a[2] - a[3]));

Compute the values dp[i] for i ≥ 3.

for(int i = 3; i <= n; i++)

{

dp[i] = min(dp[i - 1] + sq(a[i - 1] - a[i]), dp[i - 2] + 3 * sq(a[i - 2] - a[i]));

if (i < n) dp[i] = min(dp[i], dp[i - 1] + 3 * sq(a[i - 1] - a[i + 1]) + sq(a[i] - a[i + 1]));

}

Print the answer.

printf("%lld\n", dp[n]);